Determinación de Máximos y Mínimos

  

)

 Aprendizaje Personal

Determina el punto máximo y mínimo de una función, esto se obtiene resolviendo o sacando la primera derivada de la funcion el cual significa obtener el valor de "x" reemplazando su valor dependiendo el tipo de intervalo que tengamos, ya sea abierto o cerrado.

El abierto significa que no podemos tomar los valores que se encuentran dentro de el regularmente se encuentran entre paréntesis(5,6) y el intervalo cerrado significa que puedes tomar los valores que se encuentran regularmente entre corchetes[-4,6], ese valor obtenido de "x" posteriormente se reemplaza en la función principal para obtener los valores de "y".

Tambien observamos como podemos validar nuestro resultado mediante una app  llamada geogebra.org, la cual es de fácil entendimiento.

 Aprendizaje Complementario

 

MÁXIMOS Y MÍNIMOS

Los valores máximos de una función son los valores más altos de esta, mientras que los valores mínimos, como lo dice su nombre, se refiere a los valores más pequeños que dicha función puede tomar; ya sea en un intervalo determinado o de menos infinito a infinito.

 

PUNTO MÁXIMO RELATIVO Y PUNTO MÍNIMO RELATIVO:

​Debido a que muchas funciones tienen valores que van desde menos infinito a infinito es más sencillo referirse a los valores como punto máximo relativo y punto mínimo relativo, en estos dos puntos la recta tangente a la curva es completamente horizontal, por lo que su pendiente es igual a 0, aplicando los conocimientos con los que contamos podemos saber que igual, la derivada de la función va a tener el valor de 0. Estos puntos también determinan los intervalos crecientes y decrecientes.

Pasos para encontrar los puntos mínimos y máximos:

Se obtiene la derivada de la función.

Se iguala la derivada a cero para luego resolver la ecuación y así encontrar los valores de x, dichos valores son llamados valores críticos.

Se saca la segunda derivada de la función y se evalúa la función con los valores críticos previamente obtenidos. Si el resultado es menor a cero entonces tenemos un punto máximo y si es mayor a cero entonces es un punto mínimo.

Los valores críticos se evalúan en la función original para obtener el valor de "y", así determinamos las coordenadas de dichos puntos.

 

INTERVALOS CRECIENTE Y DECRECIENTE:​

Se dice que una función es creciente cuando entre mayor sea el valor de x, mayor será el valor de y. Puesto en palabras más simple va hacia delante y arriba.

En cambio, una función es decreciente cuando entre mayor sea el valor de x, menor será el valor de y. Se puede decir entre más avanza, más se sumerge.

Determinar los intervalos crecientes y decrecientes de una función:

Obtenemos la de derivada de la función.

Se determinan los valores críticos.

Se ubican dichos valores en una recta.

Se buscan números entre los parámetros y se sustituyen en la derivada.

*Si la derivada es mayor a cero, es creciente.

*Si la derivada es menor a cero, es decreciente.

CONCAVIDAD:

​Característica de una curva en el entorno de un punto en el que la tangente no la atraviesa. Se dice que dicha curva, en el punto dado, presenta una concavidad hacia el lado donde no se encuentra la tangente. la concavidad puede ser determinada por medio de la segunda derivada.

Una función es cóncava hacia arriba cuando las rectas tangentes a dicha función están por debajo de la curva.

De forma inversa, una función es cóncava hacia abajo cuando las rectas tangentes a dicha función están encima de la curva.

En un punto de la función cambia la concavidad, este punto es conocido como punto de inflexión.

PUNTO DE INFLEXIÓN:

El punto de inflexión es aquel en donde la recta tangente atraviesa la gráfica de la función y ocurre un cambio de curvatura ya sea de cóncava a convexa o convexa a cóncava.

Por lo tanto este punto nos representa el cambio de concavidad en la función.

Con este punto podemos determinar los intervalos de concavidad.

Video explicativo

Referencias:

Información valiosa tomada de:

CÁLCULO DIFERENCIAL - MÁXIMOS Y MÍNIMOS (weebly.com)

Derivadas Implícitas

 

 Aprendizaje Personal

Se realiza como una ecuación de primer o segundo grado que es despejando, sin embargo aplicando las derivaciones.

en este caso se debe encontrar la dy / dx y es así como debes obtener el resultado.

 Aprendizaje Complementario

Introducción

En esta entrada estudiaremos dos conceptos que probablemente te suenen familiares: las derivadas implícitas y las derivadas de orden superior. Una vez los hayamos comprendido, tendremos muchos más casos en los cuales podremos aplicar la derivada empleando todas las herramientas que se han desarrollado hasta este punto.

Derivadas implícitas

A las funciones que se pueden expresar de la forma 𝑦=𝑓(𝑥) definidas en un intervalo las llamamos funciones explícitas; sin embargo, en ocasiones nos encontramos con funciones que no están expresadas de esta forma. Por ejemplo, en un curso de geometría analítica se estudia la ecuación que describe una parábola vertical: 4𝑝(𝑦−𝑘)=(𝑥−ℎ)2. Esta forma, la llamaremos función implícita, y aunque en este caso podríamos despejar 𝑦 para obtener una función explícita, no siempre es posible obtenerla.

Ejemplo 1.

En el siguiente ejemplo, 𝑦 depende de 𝑥 y se busca calcular la derivada de 𝑦.

𝑥3+2𝑥2𝑦+𝑥𝑦2+𝑦3=0.

Aunque no tengamos una función explícita, esto no limita la posibilidad de encontrar la derivada de 𝑦.

(𝑥3+2𝑥2𝑦+𝑥𝑦2+𝑦3)′=(0)′.(𝑥3)′+(2𝑥2𝑦)′+(𝑥𝑦2)′+(𝑦3)′=0.3𝑥2+2𝑥2(𝑦)′+2(𝑥2)′𝑦+𝑥(𝑦2)′+(𝑥)′𝑦2+3𝑦2𝑦′=0.3𝑥2+2𝑥2𝑦′+4𝑥𝑦+2𝑥𝑦𝑦′+𝑦2+3𝑦2𝑦′=0.⇒3𝑥2+4𝑥𝑦+𝑦2+𝑦′(2𝑥2+2𝑥𝑦+3𝑦2)=0.⇒𝑦′=–3𝑥2+4𝑥𝑦+𝑦22𝑥2+2𝑥𝑦+3𝑦2.

Notemos que es complicado saber respecto a que variable estamos derivando, por ello, particularmente para las derivadas implícitas es usual emplear la notación 𝑑𝑦𝑑𝑥=𝑦′.

Video explicativo

Referencias:

Información valiosa tomada de:

Cálculo Diferencial e Integral I: Derivadas implícitas y de orden superior - El blog de Leo (nekomath.com)

Derivadas Exponenciales y Logaritmicas

 

Aprendizaje Complementario

Las funciones exponenciales y logarítmicas son conceptos fundamentales en el ámbito de las matemáticas y la ciencia. Estas funciones tienen propiedades únicas que las distinguen de otras funciones y desempeñan un papel crucial en una variedad de aplicaciones. En este artículo, exploraremos la definición de derivadas para funciones exponenciales y logarítmicas, así como su importancia en el cálculo y otros campos de estudio.

 

¿Qué son las funciones exponenciales?

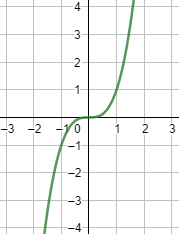
Las funciones exponenciales se definen como aquellas en las que la variable independiente aparece en el exponente. Matemáticamente, una función exponencial tiene la forma f(x) = a^x, donde “a” es la base de la función y “x” es la variable independiente. Estas funciones crecen rápidamente a medida que x aumenta, lo que las hace útiles para modelar fenómenos de crecimiento acelerado, como la población, las epidemias y las finanzas. La constante “e” es una base especial en las funciones exponenciales y es la base del logaritmo natural.

 

¿Qué son las funciones logarítmicas?

Leer másFunciones logarítmicas y exponenciales: todo lo que necesitas saber

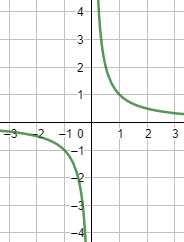
Las funciones logarítmicas son inversas de las funciones exponenciales. Mientras que las funciones exponenciales implican la exponenciación, las funciones logarítmicas involucran la operación inversa, la logaritmación. La forma general de una función logarítmica es f(x) = log_a(x), donde “a” denota la base del logaritmo. Estas funciones se utilizan para modelar situaciones en las que el crecimiento es más lento y se desean escalas de medida logarítmicas, como en la química, la física y la ingeniería.

 

Derivadas de funciones exponenciales

Quizás también te interese:  Domina las técnicas esenciales para evaluar límites en cálculo diferencial

Ahora que hemos establecido una comprensión básica de las funciones exponenciales, es esencial comprender cómo calcular sus derivadas. La derivada de una función exponencial f(x) = a^x, donde “a” es una constante positiva, es de particular interés en el contexto del cálculo diferencial. La derivada de una función describe la tasa de cambio instantáneo de la función en un punto dado y es fundamental para comprender el comportamiento de la función en cuestión.

 

Leer másDomina las técnicas esenciales para evaluar límites en cálculo diferencial

Para calcular la derivada de f(x) = a^x, utilizamos la definición de la derivada con límites. Aplicando el límite cuando h tiende a cero en la expresión [f(x + h) – f(x)]/h, obtenemos la derivada de la función exponencial como f'(x) = a^x * ln(a), donde “ln(a)” representa el logaritmo natural de la base “a”. Esta fórmula revela que la derivada de una función exponencial es proporcional a la función original y depende de la base de la exponencial.

 

Propiedades de las derivadas de funciones exponenciales

Las derivadas de funciones exponenciales tienen propiedades interesantes que las distinguen de otras funciones. Una de las propiedades clave es que la función exponencial e^x tiene una derivada igual a ella misma, es decir, (e^x)’ = e^x. Esta característica es particularmente significativa en la teoría de ecuaciones diferenciales y modelado matemático, ya que las funciones exponenciales emergen naturalmente en una variedad de contextos.

 

Otra propiedad notable es que la base “e” tiene una importancia especial en el cálculo, ya que las funciones exponenciales con base “e” tienen derivadas simples y elegantes. Esta conexión entre la constante “e” y las derivadas proporciona un fundamento fundamental para la aplicación de funciones exponenciales en el análisis matemático y la ingeniería.

 

Derivadas de funciones logarítmicas

Ahora nos dirigimos hacia la derivada de las funciones logarítmicas. Al igual que con las funciones exponenciales, comprender la derivada de una función logarítmica es esencial para analizar su comportamiento y aplicarla en diversos contextos. La derivada de la función logarítmica f(x) = log_a(x) se obtiene utilizando técnicas similares a las aplicadas en el caso de las funciones exponenciales.

 

 

Cálculo de la derivada de una función logarítmica

La derivada de la función logarítmica f(x) = log_a(x) se puede calcular aplicando la definición de la derivada con límites. Al evaluar el límite cuando h tiende a cero en la expresión [f(x + h) – f(x)]/h, obtenemos la derivada de la función logarítmica como f'(x) = 1/(x * ln(a)), donde “ln(a)” representa el logaritmo natural de la base “a”. Esta fórmula revela que la derivada de una función logarítmica depende del logaritmo natural de la base y está relacionada inversamente con la variable independiente “x”.

 

Propiedades de las derivadas de funciones logarítmicas

Las derivadas de funciones logarítmicas también tienen propiedades significativas que influyen en su aplicación y comprensión. Una de estas propiedades es que la derivada de la función logarítmica es siempre positiva para x > 1 y siempre negativa para 0 < x < 1. Esta característica refleja el comportamiento de las funciones logarítmicas en términos de su pendiente y proporciona información importante sobre su crecimiento y decrecimiento en diferentes intervalos.

 

Además, la derivada de la función logarítmica f(x) = ln(x) con base e, es igual a 1/x, lo que sugiere que la tasa de cambio instantáneo de la función logarítmica está inversamente relacionada con la variable x. Estas propiedades son fundamentales para comprender cómo las funciones logarítmicas modelan fenómenos en diversas disciplinas, como la economía, la biología y la estadística.

Aplicaciones de las derivadas de funciones exponenciales y logarítmicas

Las derivadas de funciones exponenciales y logarítmicas tienen una amplia gama de aplicaciones en diversos campos. En la física, por ejemplo, las funciones exponenciales modelan el decaimiento radioactivo y el crecimiento exponencial de poblaciones. Las derivadas de estas funciones son fundamentales para comprender la tasa de desintegración y el crecimiento poblacional en un momento dado, lo que tiene implicaciones significativas en la investigación y la ingeniería.

 

En el ámbito de las finanzas, las funciones exponenciales modelan el crecimiento compuesto de las inversiones y la deuda. Las derivadas de estas funciones informan sobre la tasa de cambio en el valor de una inversión o el ritmo al que una deuda acumula intereses, lo que es crucial para la toma de decisiones financieras informadas.

 

Las funciones logarítmicas, por otro lado, se utilizan en aplicaciones como la medición de pH en química, la magnitud de terremotos en geología y la interpretación de datos en la biología. Las derivadas de las funciones logarítmicas proporcionan información vital sobre la tasa de cambio en estos contextos, lo que contribuye a la comprensión y el análisis de fenómenos naturales y artificiales.

 

En resumen, las derivadas de funciones exponenciales y logarítmicas tienen un impacto significativo en la comprensión y el modelado de fenómenos en una amplia gama de disciplinas, lo que subraya su importancia en el ámbito académico y profesional.

 

Conclusion

En este artículo, hemos explorado la definición de derivadas para funciones exponenciales y logarítmicas, así como su importancia en diversas áreas de estudio. Hemos examinado cómo calcular las derivadas de estas funciones y hemos destacado sus propiedades distintivas. Además, hemos explorado varias aplicaciones de las derivadas de funciones exponenciales y logarítmicas en campos como la física, las finanzas, la química y la biología.

 

Al comprender las derivadas de funciones exponenciales y logarítmicas, los estudiantes y profesionales pueden adquirir una sólida base para enfrentar problemas y fenómenos complejos en el mundo real. Esta comprensión no solo tiene implicaciones académicas, sino que también es invaluable en la resolución de problemas prácticos y en la toma de decisiones informadas en una variedad de campos.

 

En última instancia, la capacidad de calcular y aplicar derivadas de funciones exponenciales y logarítmicas es esencial para el avance del conocimiento y la innovación en numerosos dominios. Con un sólido entendimiento de estas derivadas, los individuos están mejor equipados para abordar desafíos matemáticos, científicos y de ingeniería, y para contribuir al progreso de la sociedad en su conjunto.

Referencias:

Información valiosa tomada de:

https://matematizame.com/

Reglas Trigonométricas

 

 Aprendizaje Personal

Se tiene que conocer la función o funciones que se están por resolver para saber que tipos de regla o formula es la que tienes que aplicar, adicional lo que vi en clase es aplicar los conocimientos algebraicos que previamente tuvimos ya sea en la prepa y en el cuatrimestre pasado.

en clase conocimos la regla del seno, que en mi parecer se me hizo sencilla y donde se nos mostro un ejemplo que para derivar utilizamos el cos U que multiplica la derivada de u, y también se vio la regla del cos U donde se usa -sen de u que multiplica la derivada de u.

 Aprendizaje Complementario

Durante nuestro estudio del cálculo diferencial hemos aprendido que las derivadas juegan un papel muy importante para las matemáticas, la física y la química, es por ello que hemos aprendido a derivar con varios ejemplos propuestos para poder aprender de la mejor forma, las derivadas trigonométricas no deben faltar en nuestro estudio completo de derivadas.

En este artículo nos centraremos solamente a derivar funciones que impliquen funciones trigonométricas, pero haciendo uso de la práctica de las reglas de derivación algebraica, y las reglas de la derivación del producto, cociente y potencia. Para ello, nuevamente comentamos que es importante tener en cuenta algunos conceptos antes de meternos de lleno a la derivación. Por ejemplo, comprender que es el argumento en una función trascendente, y por supuesto que es una función trascendente.

¿Qué es una función trascendente y qué es el argumento?

Las funciones trascendentes son aquellas funcionen que poseen algo llamado "argumento", dicho argumento es una cantidad numérica o simbólica que hacen que una función obtenga un valor, es decir, el argumento hace que la función se vuelva un valor numérico, sin el argumento la función se convierte en una función vacía, carece de valor.

Para citar un ejemplo, veamos la función coseno ( cos ), el coseno por si mismo no posee valor, necesita un argumento para que éste pueda tener un valor real, vamos agregarle el número 45 a su argumento, entonces tendríamos:

Aquí vemos que el coseno, ya adquiere un valor. Entonces en conclusión, el 45 es el argumento del coseno.

Las funciones trigonométricas, logarítmicas, exponenciales e inversas son funciones trascedentes.

Lo común es que el argumento esté siempre en paréntesis después de la función principal, a veces se omite pero debemos entender cual es la función y cual el argumento.

⚠️ No confundir 

Es normal confundir el argumento con otra función si no se agrupan los términos correctamente, aquí abajo vemos un claro ejemplo del error común con los argumentos.

Veamos otros dos errores comunes, que el alumno puede confundir. Es mejor aclarar cuando una función está elevada a una potencia, y cuando es el argumento que está elevado a una potencia.

Teniendo en cuenta estos puntos importantes y advertencias, ahora si podemos empezar por aprender las reglas de derivación para funciones trigonométricas y posteriormente comenzar a derivar desde cero.

Fórmulas Para las Derivadas de Funciones Trigonométricas

Video explicativo

Referencias:

Información valiosa tomada de:

Carlos Julián es Ingeniero Mecatrónico, profesor de Física y Matemáticas.

Derivada de Funciones Trigonométricas - Fisimat

Reglas de la Derivación

   

 Aprendizaje Personal

Con estas reglas nos ensena una manera mas practica de resolver las derivadas dejando un poco atrás los limites, sin embargo creo que es importante identificar que tipo de regla debemos utilizar para cada uno de los ejercicios que vayamos a realizar.

Un punto clave el cual vimos en clase, es visualizar que tipo de operación se esta realizando y así saber la regla que debemos utilizar.

 Aprendizaje Complementario

¿Qué son las reglas de derivación?

Las reglas de derivación son el conjunto de indicaciones a seguir para encontrar la derivada ordinaria de una función de variable real f(x).

La derivada ordinaria de la función f(x), denotada como f’(x), se interpreta como la tasa de cambio instantánea de dicha función respecto a la variable x. Gráficamente, la derivada es la pendiente de la recta tangente a la curva de f(x), calculada en un punto dado cuya coordenada es xo, tal como se representa en la figura de abajo.

Ahora bien, analíticamente la derivada se calcula a través del siguiente límite:

Entonces, cada vez que se requiera la derivada de alguna función, habría que evaluar el límite como se indica. Sin embargo, existen las reglas de derivación, que se memorizan fácilmente con un poco de práctica y ahorran el trabajo de calcular el límite, lo cual en algunos casos es engorroso.

Referencias:

Información valiosa tomada de:

Fanny Zapata Licenciada en Física, con mención en Física Experimental

Última edición el 3 de mayo de 2021, © Lifeder 2024 | All Rights reserved.

Definición de la Derivada

 

 Aprendizaje Personal

El tema es interesante ya que la derivada es la que nos permite encontrar la velocidad en un punto exacto, o también se puede decir que es la que nos permite encontrar la recta tangente a una función dada.

Esto es importante ya que en los procesos regularmente no existe una velocidad promedio, sino que va cambiando de acuerdo al tiempo, para estos ejercicios utilizamos una función que se determina de la siguiente manera:

Recordemos que la "h" tambien en algunos libros la podemos encontrar como un triangulo y una x, que a esto de le llama delta equis.

 Aprendizaje Complementario

¿Qué es una derivada?

Se utiliza en matemática para el cálculo de respuestas de una función a la que se le están alternando sus valores iniciales, el cual está representada gráficamente como una línea recta superpuesta sobre otra curva (función) y el valor de esta pendiente respecto al eje sobre el cual está siendo evaluada la función recibe el nombre de derivada.

¿Para qué sirve?

Sirven para garantizar u optimizar sistemas que se expresan con funciones más o menos complejas.
Uso de las derivadas en la vida diaria

No solo cumple un papel fundamental en el área de la matemática, sino también en diversas ciencias como la física, mecánica, biología, en el estudio de la medicina y la economía.

Una forma más sencilla de comprenderlas es saber que estas representan razones de cambio, en ingeniería por ejemplo sirve para calcular la variación de la temperatura en un tubo cuando aumenta la presión.

Otro ejemplo sería para calcular cuánto tiempo le durará la batería a un celular en función al cambio de consumo de corriente durante una llamada.
Derivada de una función real

La función f es la función f’ definida por:

Para todo x donde exista este límite.

Cuando estamos interesados particularmente en el valor de la derivada f’ en x=a reescribimos la definición así:

Se observa que x→a cuando h→0 si el límite de la definición existe decimos que la función f es derivable o diferenciable en x=a. el proceso de encontrar la derivada (f’) se llama derivación de f.

Referencias:

Información valiosa tomada de:

Yolijose Rivas

Profesora de Matemática, Egresada de la Universidad Pedagógica Experimental Libertador (UPEL) - Venezuela, http//www.matemente.com/derivada/#GeneratedCaptionsTabForHeroSec#:~:text=Una%20derivada

Continuidad de una funcion

 

 Aprendizaje Personal

Una función se puede identificar si es continua, directamente en una gráfica, y a simple vista se puede decir que es sencillo identificarla, ya que los trazos se realizan sin una separación. pero cuando se trata de identificar analíticamente con la función F(x) ahí es donde se pone un puede poner un poco complejo desde mi punto de vista y es ahí donde hay que resolver, y definimos que una función es continua cuando los 3 limites tienen el mismo valor.

La discontinuidad, de igual manera se puede identificar gráficamente pues muy rápido ya que existe una separación entre los trazos, y para identificarla de forma analítica basta tener un límite de diferente valor a los demás.

 Aprendizaje Complementario

1. Concepto de continuidad


Intuitivamente, una función es continua si su gráfica puede dibujarse de un solo trazo, es decir, sin levantar el lápiz del papel.


Ejemplo de función continua: f(x)=x3𝑓(𝑥)=𝑥3.

Gráfica:





Ejemplo de función no continua: f(x)=1/x𝑓(𝑥)=1/𝑥.

Gráfica:


Definición formal:


La función f𝑓 es continua en el punto c𝑐 si

limx→cf(x)=f(c)lim𝑥→𝑐𝑓(𝑥)=𝑓(𝑐)

La función f𝑓 es continua si es continua en todos los puntos.

Por ejemplo, la función f(x)=1/x𝑓(𝑥)=1/𝑥 no es continua en x=0𝑥=0 porque no existe f(0)𝑓(0).
Observaciones:

En realidad, para hablar de continuidad en un punto a𝑎, debería ser indispensable que el punto a𝑎 pertenezca al dominio de la función.

Por ejemplo, el dominio de f(x)=1/x𝑓(𝑥)=1/𝑥 es R−{0}𝑅−{0} y la función es continua en su dominio. Sin embargo, no existe el límite de f(x)𝑓(𝑥) cuando x→0𝑥→0 ni existe f(0)𝑓(0), por lo que decimos que f𝑓 no es continua en x=0𝑥=0.

Como normalmente consideramos a todas las funciones como f:R→R𝑓:𝑅→𝑅, tenemos que calcular primero el dominio de la función y, después, la continuidad en el dominio.

Funciones polinómicasf(x)=amxm + am−1xm−1 +𝑓(𝑥)=𝑎𝑚𝑥𝑚 + 𝑎𝑚−1𝑥𝑚−1 ++ ... + a1x + a0+ ... + 𝑎1𝑥 + 𝑎0

Son continuas en todos los reales.

Funciones racionalesf(x)=p(x)q(x)𝑓(𝑥)=𝑝(𝑥)𝑞(𝑥)

Son continuas en todos los reales excepto en los que anulan al denominador.

Funciones exponencialesf(x)=ax𝑓(𝑥)=𝑎𝑥

Como regla general, son continuas en todos los reales. Cuando la base es no positiva, a≤0𝑎≤0, puede haber complicaciones.

Funciones logarítmicasf(x)=log(x)𝑓(𝑥)=log⁡(𝑥)

Son continuas en todos los reales positivos.

Funciones irracionalesf(x)=n√x𝑓(𝑥)=𝑥𝑛

Si n𝑛 es par, son continuas en todos los reales. Si n𝑛 es impar, en los reales positivos.

Funciones trigonométricas

El seno y el coseno son continuas en todos los reales. La tangente no es continua en π/2+nπ𝜋/2+𝑛𝜋 para todo entero n𝑛.

La mayoría de las funciones que veremos son combinaciones de las anteriores, así que es recomendable aprender su continuidad.

Referencias:

Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.

Limites Algebraicos

 Aprendizaje Personal

Es un tema que, en lo personal interesante, pero a la vez con demasiada información a trabajar, en mis palabras un límite algebraico es básicamente encontrar el valor de (Y) cuando (X) tiene un determinado valor, que normalmente se llama "cuando x tiende a" y esto se puede observar en una gráfica como la siguiente:

 Aprendizaje Complementario

¿Qué son los límites algebraicos y cómo se calculan?

Son el valor al que tiende una función cuando la variable independiente se aproxima a un cierto número. Se calculan evaluando la función en valores cercanos al número al que se quiere encontrar el límite, o utilizando propiedades como factorización, racionalización o el uso de la regla de L'Hôpital en casos indeterminados.

¿Cuál es la importancia de comprender los límites algebraicos en matemáticas?

La importancia de comprender los límites en matemáticas radica en su papel fundamental para entender el comportamiento de funciones, calcular pendientes y determinar valores límite en diferentes situaciones matemáticas y científicas.

¿Cómo se pueden aplicar los límites en el contexto de la resolución de problemas matemáticos?

Los límites algebraicos se pueden aplicar en la resolución de problemas matemáticos para evaluar el comportamiento de una función en puntos específicos y para encontrar valores límite en situaciones que tienden al infinito o a cero.

Referencias:

Información valiosa tomada de:

Autor Gabriela Vargas © 2024 - Matematicas.CLICK sitio web:http//matematicas.click/limites-algebraicos

CONOCIMIENTO PREVIO PARA CALCULO

OPERACIONES ALGEBRAICAS 

 Aprendizaje Personal

Son aquellas expresiones en donde podemos utilizar, números, letras y símbolos, donde se pueden realizar, sumas, restas, multiplicación, división, potenciación radicación, un ejemplo puede ser:

2X + 3Y = 15

 Aprendizaje Complementario

Al escribir todas las operaciones que veremos a continuación, te comentaré que usamos símbolos de agrupación, el más conocido es el paréntesis ( )( ). El cual significa que los términos encerrados en el paréntesis deben ser considerados como un sólo número. Te muestro más símbolos de agrupación: corchetes o paréntesis rectangular [ ][ ], llave { }{ } y la barra o vínculo ‾ el cual se coloca arriba de los términos a agrupar: 1+2+3‾1+2+3​.

Referencias:

Información valiosa tomada de:

Lehmann, C. (2012). Álgebra, D.F. México, Limusa. operaciones algebraicas [web log post]recuperado de http//rbjlabs.com/algebra/operaciones-algebraicas/

FACTORIZACION

Aprendizaje Personal

Es la manera de simplificar una expresion algebraica, para mi es hacerla de una manera mucho mas sensilla, simple y entendible, ejemplo:

(x+1)(x+1) = x² + 2x +1

 Aprendizaje Complementario

En el campo de las matemáticas, la factorización es definida como la ruptura o descomposición que se presenta en un determinado número en un producto diferente o factores, los cuales, en el momento de ser multiplicados, dan como resultado el número original. Con este tipo de método matemático, es posible reducir cualquier ecuación de tipo algebraica en una forma más sencilla en la cual, las ecuaciones son representadas como el producto de factores.

Referencias:

                                                       Información valiosa tomada de:
                 Briceño V., Gabriela. (2021). Factorización. Recuperado el 22 febrero, 2024, de Euston96:                                                                   https://www.euston96.com/factorizacion/

Aprendizaje Personal

Son operaciones matemáticas que nos ayudan a resolver cantidades fraccionarias, existen 2 tipos, la que tenemos con denominadores iguales y las que tienen diferente denominador.

             Cuando es el mismo denominador, se suma o resta el numerador y el denominados pasa igual.

            Cuando los denominadores son diferentes se debe sacar el Minimo Comun Denominados.

 Aprendizaje Complementario

La suma y la resta de fracciones son fáciles de calcular, aunque se realizan de forma distinta según si los denominadores de las fracciones son iguales o distintos.

Antes que nada, debemos recordar que el numerador es el número sobre la raya de la fracción y el denominador es el que esta debajo de la raya. Por ejemplo,

Cuando el denominador es distinto, tenemos que realizar más operaciones: cambiar las fracciones por otras equivalentes para que tengan el mismo denominador y así poder sumarlas (sumando sus numeradores). Vamos a explicar dos métodos:

Método 1

Consiste en utilizar el mínimo común múltiplo (mcm) de los denominadores:

siendo $s$ el mínimo común múltiplo de los denominadores $a$ y $b$.

Se utiliza el mcm de los denominadores como denominador común y se cambian los numeradores por el resultado de dividir el nuevo denominador entre el antiguo y multiplicarlo por el antiguo numerador.

Nota: la fórmula parece más díficil de lo que es.

Por ejemplo,

 

Referencias:

Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.

Aprendizaje Personal

Son aquellas reglas que nos sirven para hallar el valor de una expresión más rápidamente.

Aprendizaje complementario

Aprendizaje ComplementarioLos exponentes son una forma de expresar la multiplicación de una expresión por sí misma un cierto número de veces. Al evaluar y simplificar exponentes, utilizamos la Leyes de los exponentes, una serie de reglas que nos ayudan a encontrar el valor de una expresión más rápidamente.

La ley de los exponentes en la multiplicación, que nos dice que para multiplicar potencias de la misma base se suman los exponentes y se aplica de la misma manera. cuando las cantidades que se multiplican tienen exponentes negativos o fraccionarios.

 

                                              Referencias:

Información valiosa tomada de:

Baldor A. (2015). Algebra. México D.F.: Grupo Editorial Patriahttps://www.uaeh.edu.mx/docencia/P_Presentaciones/huejutla/sistemas/2017/Leyes_de_los_Exponentes.

Aprendizaje Personal

Son aquellas reglas que nos sirven para saber si nuestro resultado debe ser positivo o negativo, algo que aprendí de esto es que debemos de extremar cuidado ya que puedes tener la operación correcta, pero si tienes un error en el signo cambia completamente y tendrías un error muy común.

Aprendizaje Complementario

Las Leyes de los Signos proporcionan una manera rápida de realizar operaciones aritméticas y algebraicas tomando en cuenta el signo que debe prevalecer en la operación.

Las Leyes de los Signos funcionan principalmente en operaciones de multiplicación y división. En operaciones elementales como la suma y la resta, el signo que preservamos es el que tiene el elemento con valor absoluto más grande.

Referencias:

Información valiosa tomada de:

Copyright © 2024 Matematicas.org.mx. Theme by www.matematicas.org.mx/algebra/leyes-de-los-signos/

Aprendizaje Personal

Es una fórmula que nos ayuda a resolver ecuaciones, que prácticamente debemos reemplazar las letras por el valor asignado y resolver la formula.

Aprendizaje Complementario

La expresión canónica de una ecuación cuadrática -o de segundo grado- es

ax2+bx+c=0𝑎𝑥2+𝑏𝑥+𝑐=0

Resolverla significa encontrar todos aquellos números reales, que cumplen la igualdad cuando sustituyen a x𝑥 en la ecuación. Cada uno de esos números, se llama solución de la ecuación. También es frecuente llamarles raíces o ceros de la ecuación.

Existen varios métodos para resolver estas ecuaciones, quizá los más conocidos tienen que ver con factorizar la expresión, pero esto no siempre es una tarea sencilla.

Las ecuaciones cuadráticas son conocidas desde la antigüedad y la historia registra varios métodos de resolución. La primera solución completa -es decir que abarca todos los casos de ecuaciones- la desarrolló el matemático persa musulmán Al-Khwarizmi en el siglo IX de nuestra era.

Desde entonces, los estudiosos de las matemáticas han buscado estrategias generales para resolver ecuaciones. La intención, ha sido encontrar una fórmula que describa explícitamente cuáles son todas las soluciones, en términos de los coeficientes de la ecuación. Si hay una colección de ecuaciones para las que existe tal fórmula, se dice que esas ecuaciones son solubles por radicales.

Desafortunadamente, no todas las ecuaciones son solubles por radicales. Fue hasta el siglo XIX, cuando el matemático francés Evariste Galois estableció las condiciones que deben cumplir las ecuaciones que sí lo son.

Las ecuaciones cuadráticas sí son solubles por radicales, por lo que sí existe una fórmula que describe explícitamente todas las soluciones en términos de los coeficientes. Esta es conocida como la la fórmula general para resolver ecuaciones cuadráticas. Te la presentamos aquí:

x1,2=−b±√b2−4ac2a𝑥1,2=−𝑏±𝑏2−4𝑎𝑐2𝑎

Observa que hay dos posibles soluciones, una por cada signo de la raíz cuadrada, por esto la x𝑥 aparece con dos subíndices: uno por cada solución.

Relacionemos los coeficientes de la ecuación con los parámetros de la fórmula:

a𝑎 es el coeficiente de x2𝑥2, el término cuadrático

b𝑏 es el coeficiente de x𝑥, el término lineal

c𝑐 es el número que no está acompañando a la incógnita, le llamamos término independiente.

 

Referencias:

Información valiosa tomada de:

Hecho en México. B@UNAM de la Coordinación de Universidad Abierta, Innovación Educativa y Educación a Distancia de la UNAM / UNAM./

Aprendizaje Personal

Es aquella en la que la incógnita aparece por lo menos 1 vez elevada al cuadrado, es el exponente el que toma la responsabilidad de hacernos saber de qué grado es una ecuación.

Aprendizaje Complementario

En general, las ecuaciones de segundo grado son aquellas donde la x aparece elevada a 2 en alguno de sus términos.

Pueden ser ecuaciones de segundo grado completas o incompletas, en función de si tienen todos su términos o no. Aquí me voy a centrar en explicarte las ecuaciones de segundo grado completas.

Qué son las ecuaciones de segundo grado completas.

Las ecuaciones de segundo grado completas o ecuaciones cuadráticas son las que se representan de la siguiente forma:

Donde a, b y c son las constantes de la ecuación:a es el número que va siempre delante de x al cuadrado.

b es el número que va siempre delante de la x.

c es el número.

Es decir, las ecuaciones de segundo grado completas son las que tienen término con x elevada a 2, término con x elevada a 1 (o simplemente la x). Si faltara alguno de estos términos, estaríamos hablando de ecuaciones de segundo grado incompletas, que se resuelven con otro procedimiento distinto.

Al ser ecuaciones de segundo grado, tienen 2 soluciones. Recuerda que el grado de una ecuación es igual al número de soluciones

 

Referencias:

Información valiosa tomada de:

© 2015 - 2023 Clases de Matematicas online  https/ekuatio.com/apuntes-de-matematicas/algebra/soluciones-ecuaciones-de-segundo-grado/

Aprendizaje Personal

La verdad no recordaba bien el tema, pero con la ayuda de videos y la investigacion me ayuda a darme un refresh del tema, el cual, explicándolo de la manera más sencilla, es una serie de pasos que nos ayuda a obtener el resultado si hacer todo el procedimiento completo.

En donde producto se refiere al resultado de una multiplicación. 

Aprendizaje Complementario

Los productos notables o también conocidos como identidades notables, son un producto o expresiones algebraicas, que cumplen con ciertas reglas, que se conocen como reglas fijas, y donde el resultado obtenido lo podemos escribir con solo hacer una inspección, sin necesidad de verificar la multiplicación o recurrir a varios pasos.

Los productos notables, se puede decir que son el resultado de hacer una factorización, formada de polinomios que poseen varios términos.

En los polinomios, son de gran ayuda, ya que con el uso de sus reglas y fórmulas, permiten que el proceso sea mucho más corto y que podamos expresar un polinomio directamente sin necesidad de ir probando cada término.
Para qué se usan los productos notables?

Los productos notables los podemos usar para realizar operaciones algebraicas de una manera más rápida, sin necesidad de hacer una comprobación de la multiplicación realizada.

En otros casos son utilizados porque ayudan al encontrar: medidas, o en el cálculo de área, superficies, e intensidades en el área de la ingeniería.

 

Referencias:

Información valiosa tomada de:

© COPYRIGHT 2019 https//wikimat.es/polinomios/productos-notables//