Continuidad de una funcion

 

 Aprendizaje Personal

Una función se puede identificar si es continua, directamente en una gráfica, y a simple vista se puede decir que es sencillo identificarla, ya que los trazos se realizan sin una separación. pero cuando se trata de identificar analíticamente con la función F(x) ahí es donde se pone un puede poner un poco complejo desde mi punto de vista y es ahí donde hay que resolver, y definimos que una función es continua cuando los 3 limites tienen el mismo valor.

La discontinuidad, de igual manera se puede identificar gráficamente pues muy rápido ya que existe una separación entre los trazos, y para identificarla de forma analítica basta tener un límite de diferente valor a los demás.

 Aprendizaje Complementario

1. Concepto de continuidad


Intuitivamente, una función es continua si su gráfica puede dibujarse de un solo trazo, es decir, sin levantar el lápiz del papel.


Ejemplo de función continua: f(x)=x3𝑓(𝑥)=𝑥3.

Gráfica:





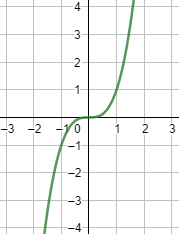
Ejemplo de función no continua: f(x)=1/x𝑓(𝑥)=1/𝑥.

Gráfica:


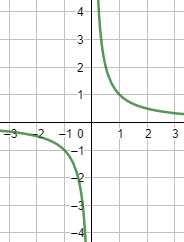
Definición formal:


La función f𝑓 es continua en el punto c𝑐 si

limx→cf(x)=f(c)lim𝑥→𝑐𝑓(𝑥)=𝑓(𝑐)

La función f𝑓 es continua si es continua en todos los puntos.

Por ejemplo, la función f(x)=1/x𝑓(𝑥)=1/𝑥 no es continua en x=0𝑥=0 porque no existe f(0)𝑓(0).
Observaciones:

En realidad, para hablar de continuidad en un punto a𝑎, debería ser indispensable que el punto a𝑎 pertenezca al dominio de la función.

Por ejemplo, el dominio de f(x)=1/x𝑓(𝑥)=1/𝑥 es R−{0}𝑅−{0} y la función es continua en su dominio. Sin embargo, no existe el límite de f(x)𝑓(𝑥) cuando x→0𝑥→0 ni existe f(0)𝑓(0), por lo que decimos que f𝑓 no es continua en x=0𝑥=0.

Como normalmente consideramos a todas las funciones como f:R→R𝑓:𝑅→𝑅, tenemos que calcular primero el dominio de la función y, después, la continuidad en el dominio.

Funciones polinómicasf(x)=amxm + am−1xm−1 +𝑓(𝑥)=𝑎𝑚𝑥𝑚 + 𝑎𝑚−1𝑥𝑚−1 ++ ... + a1x + a0+ ... + 𝑎1𝑥 + 𝑎0

Son continuas en todos los reales.

Funciones racionalesf(x)=p(x)q(x)𝑓(𝑥)=𝑝(𝑥)𝑞(𝑥)

Son continuas en todos los reales excepto en los que anulan al denominador.

Funciones exponencialesf(x)=ax𝑓(𝑥)=𝑎𝑥

Como regla general, son continuas en todos los reales. Cuando la base es no positiva, a≤0𝑎≤0, puede haber complicaciones.

Funciones logarítmicasf(x)=log(x)𝑓(𝑥)=log⁡(𝑥)

Son continuas en todos los reales positivos.

Funciones irracionalesf(x)=n√x𝑓(𝑥)=𝑥𝑛

Si n𝑛 es par, son continuas en todos los reales. Si n𝑛 es impar, en los reales positivos.

Funciones trigonométricas

El seno y el coseno son continuas en todos los reales. La tangente no es continua en π/2+nπ𝜋/2+𝑛𝜋 para todo entero n𝑛.

La mayoría de las funciones que veremos son combinaciones de las anteriores, así que es recomendable aprender su continuidad.

Referencias:

Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.