
Aprendizaje Personal
Recordé nuevamente como realizar las integrales, que fue un poco de mis complicaciones al tener que realizar ambas operaciones en una misma ecuación(diferenciales e integrales), bueno aprendí básicamente a despejar las derivada de Y hacia un lado de la igualdad y las derivada de X del otro lado de la igualdad, para después realizar la integración de la ecuación , considerando que la mayoría de las veces tendremos 2 constantes que regularmente se identifica como C1 y C2 que al final de la operación se puede dejar como C ya que significa que es un numero resultante.
Aprendizaje Complementario
Método de variables separablesEl método de variables separables se utiliza cuando la ecuación diferencial puede escribirse de tal forma que las variables dependiente e independiente aparezcan una a cada lado de la igualdad. Formalmente se dice que una ecuación es de variables separables cuando puede escribirse de la forma:
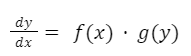
Observemos que en la expresión anterior “dx” puede pasarse multiplicando hacia la derecha mientras que g(y) puede pasarse dividiendo hacia la izquierda y de esta manera quedan las variables separadas. De forma general, podemos identificar una ecuación de variables separables cuando la derivada de la función está igualada a un producto o cociente de funciones de “x” e “y”.
Recordemos que si en una ecuación aparece la derivada de una función con el signo prima, la podemos reemplazar como un cociente de dos diferenciales:
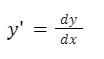
Ejemplos de ecuaciones de variables separablesVamos a ver algunos casos de ecuaciones de variables separables y cómo podemos reescribir las ecuaciones. Este es el primer paso para luego encontrar una solución.
Veamos la siguiente ecuación:
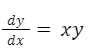
Es posible pasar el “dx” multiplicando y la “x” dividiendo y por lo tanto tener separadas las variables.
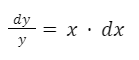
Analicemos ahora la siguiente ecuación:
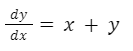
Como vemos, no es posible separar las variables a cada lado, por lo que no es una ecuación diferencial de variables separables.
Pasos para resolver una ecuación de variables separables:Separar las variables a uno y otro lado de la igualdad.
Integrar ambos lados de la ecuación, agregando las constantes de integración.
Despejar la variable dependiente “y”, de tal forma de que nos quede igualada a una función de x.
Ejemplo de resolución de ecuaciones por este métodoVeamos la siguiente ecuación:
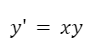
En primer lugar escribimos su derivada según la notación de Leibniz, es decir como un cociente de dos diferenciales.
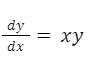
Separamos las variables:
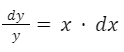
Integramos a ambos lados:
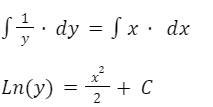
Despejamos y:
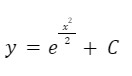
Información valiosa tomada de:
No hay comentarios:
Publicar un comentario