Problemas de Valor Inicial ED

                                                               

 

 Aprendizaje Personal

En la clase retomamos un poco el como debemos realizar las diferenciales, vimos el caso de cuando tenemos 2 términos multiplicándose, en el cual debemos aplicar la regla de la potencia para diferenciar que es du/dx=U'V * UV', después de realizar la derivación tenemos que reemplazar los valores encontrados en la ecuación principal y así corroborar si el resultado satisface la ecuación.

Aprendizaje Complementario

Ecuaciones diferenciales con valor inicial

Hemos aprendido que existen varias funciones que pueden ser solución de una ecuación diferencial debido a que las mismas contienen constantes que actúan como parámetros. Sin embargo, si se establecen ciertas condiciones como por ejemplo el hecho de la función devuelva un valor específico para un punto dado, puede restringirse la solución de tal forma que sea única.

Cómo encontrar la solución cuando hay un valor inicial

Para resolver una ecuación diferencial con valor inicial los pasos son los siguientes:

1. Encontrar la solución general
2. Reemplazar las variables por las condiciones
3. Despejar las constantes de integración y reescribir la solución

Ejemplo

Tenemos la siguiente ecuación diferencial: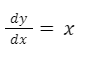



La solución a esta ecuación diferencial es la siguiente:



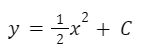
Como podemos observar, con diferentes valores de “C” encontramos distintas funciones que son solución a la ecuación diferencial.

Sin embargo,además de la ecuación diferencial podríamos tener una condición para la función solución. Por ejemplo, que la función pase por el punto (0, 1).



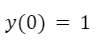
Aplicando la condición anterior a la solución obtenemos la siguiente expresión:



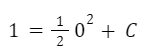
Despejamos “C”:



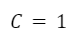
La solución particular nos queda:

Referencias:

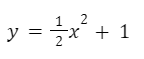
Información valiosa tomada de:

   

                                Ecuaciones diferenciales con valor inicial - Física Práctica